Competent novel strategies for Strong convergence with variational inequality and split equality crisis in fixed point theory

Abstract

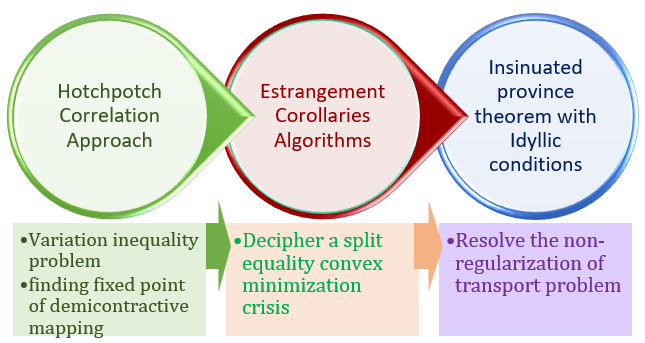
The fixed-point theory plays an important role in mathematics, including optimization, mathematical models and economic theories. This study provides new ways to overcome the challenges in the existing fixed-point theories by introducing a new Hotchpotch Correlation Approach for resolving the variation inequality problem and locating the fixed point of demi-contractive mapping. After resolving the variation inequality and the Fixed Points Problems, it incorporates the Estrangement Corollaries Algorithm, which is integrated with the inverse problem and numerical examples that are more important to understand a split equality convex minimization crisis. This increases the consistency and accuracy of the proposed work. To solve the non-regularization of the transport problem, an implied province theorem with necessary and sufficient idyllic conditions is used by deriving the restricted distributions among probability distributions. Moreover, the empirical regularized transport plan system asymptotically follows a Gaussian rule to regularize the entropy and create a limitation law for the extensively allowable Sinkhorn divergence. This suggested approach achieves strong convergence, higher consistency, and precision in the applications of fixed-point theory.

URN:NBN:sciencein.jist.2024.v12.732